We have studied extensively fluid transport in complex biological networks, mainly vasculatures. This research line was developed with Raymond Raad, Steffen Bohn, Eleni Katifori, Carl Modes, and Liat Shenhav.
Complex transport networks are hierarchical and loopy. The hierarchy establishes efficiency, the loops provide resilience to damage.
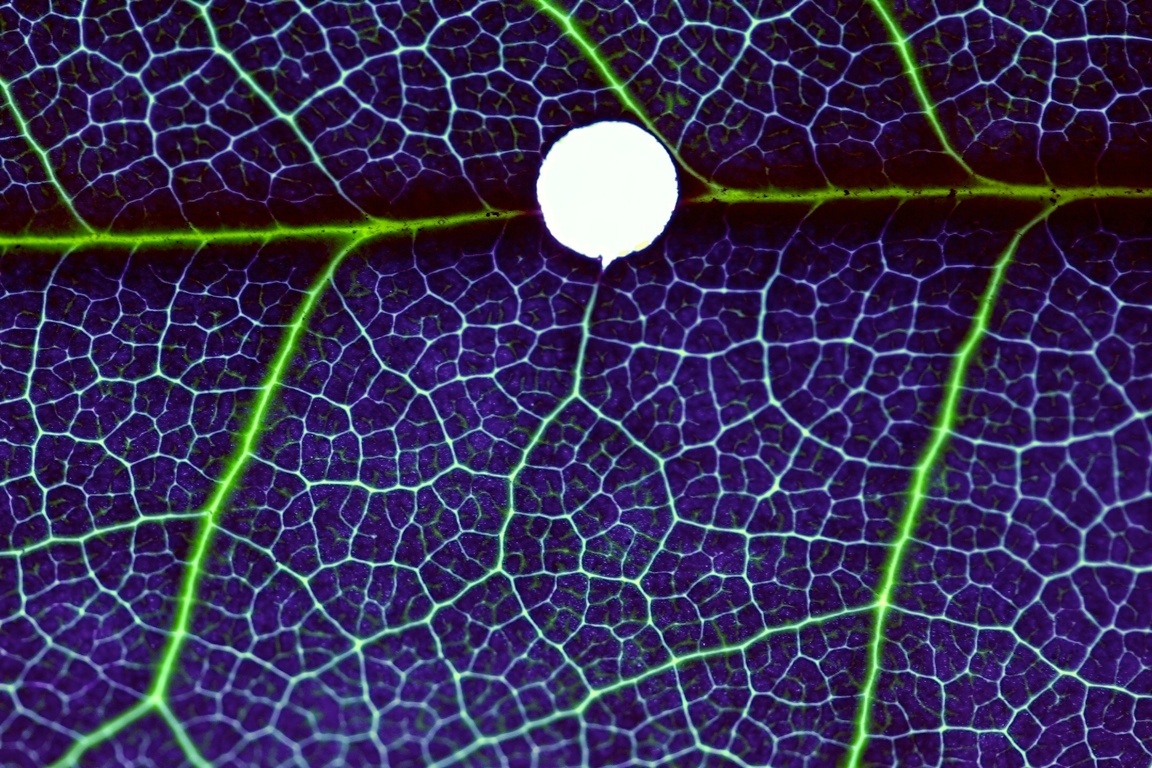
Fluorescein-injected lemon leaf with perforation on the main vein; fluid flows around the perforation. Movie by MM
Fluid transport is a central process in living beings. It displays sublinear costs, meaning that transporting twice as much is less than twice as expensive. As a result, the natural distribution strategy is hierarchical, having bigger arteries/veins from which smaller branches offshoot recursively. However, if the structure is tree-like, that is, without loops, then it is vulnerable to damage. Destroying even a small segment of a major vein will kill the entire structure. However, as shown in the movies above and below, the leaves of trees display loopy vein architecture, which allows fluid flow to be maintained even if a segment of a major vein is destroyed. Similar structure has been observed in mammalian vasculature, e.g. the surface arterioles of the brain.
Movie by Eleni Katifori
Such structures are pervasive through the kingdoms of life. Below, a movie of the slime mold Physarum polycephalum, which swishes its own cytoplasm back and forth, and constantly adapts its veins to forage.
Physarum polycephalum. Stained with di-2-anepeq. Movie MM
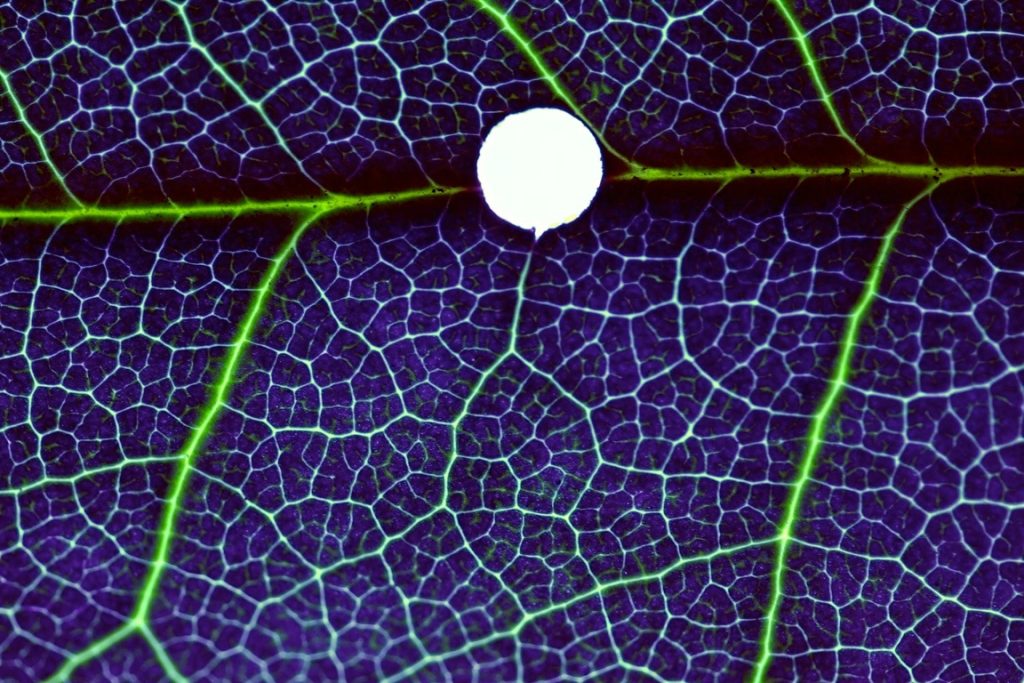
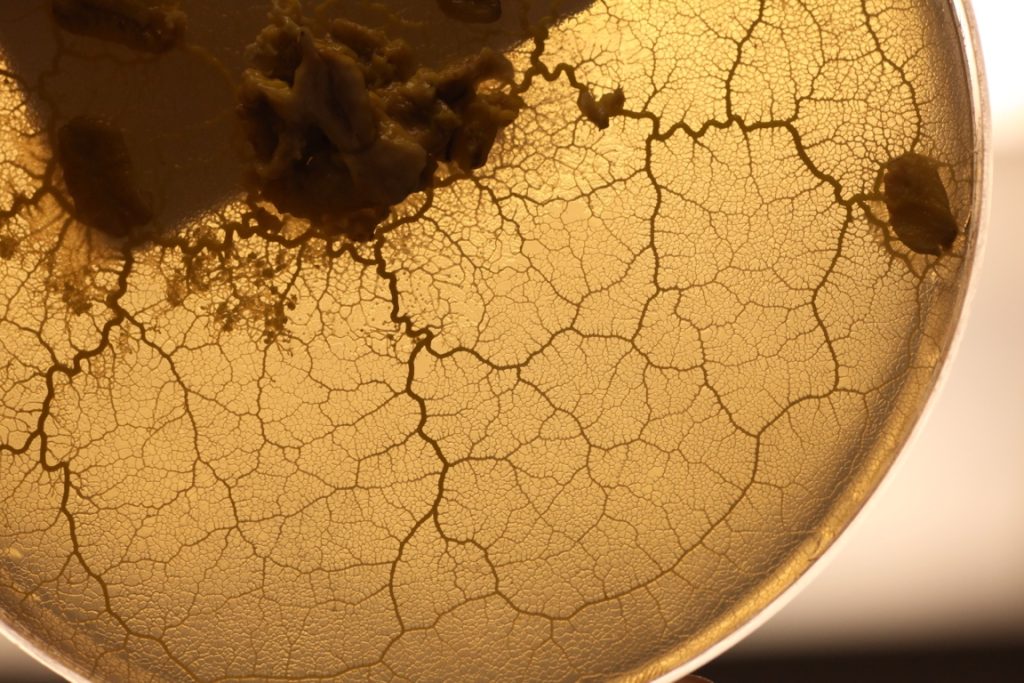
Finally, a little gallery of various structures. Structural networks, like fluid networks, share many of these features because they are networks for the distribution of stress and strain, and these propagate in ways that are not entirely unlike. Leaves are both.




Bibliography
- Bohn, S., & Magnasco, M. O. (2007). Structure, scaling, and phase transition in the optimal transport network. Physical review letters, 98(8), 088702.
- Katifori, E., Szöllősi, G. J., & Magnasco, M. O. (2010). Damage and fluctuations induce loops in optimal transport networks. Physical review letters, 104(4), 048704.
- Katifori, E., & Magnasco, M. O. (2012). Quantifying loopy network architectures. PloS one, 7(6), e37994.
- Modes, C. D., Magnasco, M. O., & Katifori, E. (2016). Extracting hidden hierarchies in 3D distribution networks. Physical Review X, 6(3), 031009.
- Gräwer, J., Modes, C. D., Magnasco, M. O., & Katifori, E. (2015). Structural self-assembly and avalanchelike dynamics in locally adaptive networks. Physical Review E, 92(1), 012801.